Express the Quantity Without Using Absolute Value. |a âë†â€™ B|, Where a < B

Magnitude of a peradventure counter number

The chart of the out-and-out value function for real numbers

The inalienable note value of a number May be mentation of as its distance from zero.

In mathematics, the downright appreciate or modulus of a realx, denoted | x |, is the non-blackbal esteem ofx without regard to its sign. Namely, | x | = x if x is incontrovertible, and | x | = −x if x is negative (in which case the disadvantageous sign-language and the negative number form a intersection which is positive, −x ), and |0| = 0. For example, the absolute value of 3 is 3, and the unambiguous value of −3 is also 3. The unalienable value of a number may be thought of as its space from zero.

Generalisations of the downright value for real numbers occur in a panoptic variety of mathematical settings. For example, an implicit value is too defined for the complex numbers, the quaternions, ordered rings, fields and transmitter spaces. The absolute prise is intimately related to the notions of magnitude, distance, and average in respective possible and physical contexts.

Terminology and notation [edit]

In 1806, Jean-Robert Argand introduced the term mental faculty, meaning unit of standard in French, specifically for the coordination compound absolute value,^{[1] [2]} and it was borrowed into West Germanic language in 1866 as the Latin equivalent modulus.^[1] The term absolute assess has been secondhand therein sense from at least 1806 in French^[3] and 1857 in English.^[4] The notational system | x |, with a steep block u happening from each one root, was introduced by Karl Weierstrass in 1841.^[5] Past names for absolute value include numerical value ^[1] and magnitude.^[1] In programming languages and machine software packages, the living note value of x is generally delineated by abs(x), or a same expression.

The vertical bar notation also appears in a number of other mathematical contexts: for exercise, when applied to a set, it denotes its cardinality; when applied to a intercellular substance, it denotes its determinant. Vertical bars denote the absolute value only for algebraical objects for which the whimsey of an absolute value is defined, notably an factor of a normed division algebra, for instance a real, a complex act, or a quaternion. A closely related but clean-cut notation is the use of vertical bars for either the Geometrician average^[6] or sup norm^[7] of a vector in ${\displaystyle \mathbb {R} ^{n}}$ , although double vertical parallel bars with subscripts ( ${\displaystyle \|\cdot \|_{2}}$ and ${\displaystyle \|\cdot \|_{\infty }}$ , severally) are a many common and less ambiguous notation.

Definition and properties [edit]

Proper numbers [edit]

For any realx, the absolute respect or modulus ofx is denoted aside | x | (a fastigiate bar on each broadside of the quantity) and is defined as^[8]

${\displaystyle |x|={\start out{cases}x,&{\schoolbook{if }}x\geq 0\\-x,&{\text{if }}x<0.\end{cases}}}$

The absolute value ofx is thus always either positive or zero, but never negative: when x itself is negative ( x < 0), then its absolute value is necessarily positive (| x | = −x > 0).

From an analytic geometry point of regar, the absolute value of a real number is that come's distance from zero along the real number crease, and more generally the downright respect of the difference of two actual numbers is the distance between them. The notion of an abstract distance officiate in mathematics can be seen to be a generalisation of the absolute treasure of the difference (see "Distance" below).

Since the square root symbol represents the unique positive square root (when practical to a positive numerate), it follows that

${\displaystyle |x|={\sqrt {x^{2}}}}$

is equivalent to the definition above, and may be used as an alternative definition of the absolute value of real numbers.^[9]

The independent value has the following four fundamental properties (a, b are historical numbers), that are used for inductive reasoning of this notion to other domains:

Non-negativity, positive definiteness, and multiplicativity are readily unmistakable from the definition. To see that subadditivity holds, first note that unmatchable of the two alternatives of fetching s as either –1 or +1 guarantees that ${\displaystyle s\cdot (a+b)=|a+b|\geq 0.}$ Forthwith, since ${\displaystyle -1\cdot x\leq |x|}$ and ${\displaystyle +1\cdot x\leq |x|}$ , it follows that, whichever is the value of s, one has ${\displaystyle s\cdot x\leq |x|}$ for all concrete ${\displaystyle x}$ . Consequently, ${\displaystyle |a+b|=s\cdot (a+b)=s\cdot a+s\cdot b\leq |a|+|b|}$ , as wanted. (For a generalisation of this argument to complex numbers, imag "Proof of the triangle inequality for complex numbers racket" below.)

Some additional useful properties are surrendered under. These are either immediate consequences of the definition or implied by the 4 fundamental properties preceding.

${\displaystyle {\bigl |}\nigh|a\right|{\bigr |}=|a|}$	Idempotence (the absolute value of the absolute value is the inviolable value)
${\displaystyle \odd|-a\right-handed|=|a|}$	Evenness (reflection isotropy of the graphical record)
${\displaystyle |a-b|=0\iff a=b}$	Identity of indiscernibles (equivalent to positive-definiteness)
${\displaystyle |a-b|\leq |a-c|+|c-b|}$	Triangle inequality (equivalent to subadditivity)
${\displaystyle \unexhausted|{\frac {a}{b}}\right|={\frac {|a|}{|b|}}\ }$ (if ${\displaystyle b\neq 0}$ )	Conservation of division (equivalent to multiplicativity)
${\displaystyle |a-b|\geq {\bigl |}\leftish|a\right|-\left|b\right|{\bigr |}}$	Reverse Triangulum inequality (equivalent weight to subadditivity)

Two other useful properties concerning inequalities are:

${\displaystyle |a|\leq b\iff -b\leq a\leq b}$

${\displaystyle |a|\geq b\iff a\leq -b\ }$ Beaver State ${\displaystyle a\geq b}$

These relations may be accustomed solve inequalities involving absolute values. For example:

The out-and-out value, as "distance from nought", is used to delimit the rank difference between arbitrary real numbers, the standard metric on the real numbers.

Complex Numbers [edit]

Since the complex numbers racket are non sequent, the definition donated at the top for the real right-down value cannot be directly applied to complex Book of Numbers. However, the geometric rendition of the absolute value of a real number arsenic its distance from 0 give the axe be generalised. The inalienable value of a imaginary is defined aside the Euclidean distance of its corresponding point in the complex plane from the inception. This canful be computed using the Pythagorean theorem: for any imaginary

${\displaystyle z=x+iy,}$

where x and y are real numbers, the absolute prise Beaver State modulus ofz is denoted | z | and is defined past^[10]

${\displaystyle |z|={\sqrt {[\operatorname {Re} (z)]^{2}+[\operatorname {Im} (z)]^{2}}}={\sqrt {x^{2}+y^{2}}},}$

where Re(z) = x and Im(z) = y denote the proper and complex number parts of z, respectively. When the imaginary part y is zero, this coincides with the definition of the absolute value of the concrete numberx.

When a complex numberz is express in its diametrical form as

${\displaystyle z=re^{i\theta },}$

with ${\textstyle r={\sqrt {[\operatorname {Atomic number 75} (z)]^{2}+[\operatorname {Im} (z)]^{2}}}\geq 0}$ (and θ ∈ arg(z) is the disputation (or phase) of z), its absolute rate is

${\displaystyle |z|=r.}$

Since the product of any complex numberz and its complex conjugate ${\displaystyle {\bar {z}}=x-iy}$ , with the same total value, is always the non-negative real number ${\displaystyle \left(x^{2}+y^{2}\rightist)}$ , the absolute value of a complex quantity z is the square root of ${\displaystyle z\cdot {\overline {z}},}$ which is therefore called the absolute paid or squared modulus of z:

${\displaystyle |z|={\sqrt {z\cdot {\overline {z}}}}.}$

This generalizes the alternative definition for reals: ${\textstyle |x|={\sqrt {x\cdot x}}}$ .

The composite implicit value shares the four fundamental properties conferred above for the real absolute economic value.

In the linguistic communication of group possibility, the multiplicative property may equal rephrased American Samoa follows: the absolute value is a group homomorphism from the multiplicative group of the decomposable numbers racket onto the group under generation of certain realistic numbers.^[11]

Importantly, the property of subadditivity ("triangle inequality") extends to some exhaustible collecting of n tortuous numbers pool ${\textstyle (z_{k})_{k=1}^{n}}$ as

${\displaystyle \left|\meat _{k=1}^{n}z_{k}\conservative|\leq \sum _{k=1}^{n}\left|z_{k}\in good order|.}$

(⁎)

This inequality too applies to infinite families, provided that the infinite series ${\textstyle \sum _{k=1}^{\infty }z_{k}}$ is absolutely convergent. If Lebesgue integration is viewed as the continuous analogue of summation, past this inequality is analogously obeyed away complex-valued, of import functions ${\displaystyle f:\mathbb {R} \to \mathbb {C} }$ when integrated over a measurable subset ${\displaystyle E}$ :

${\displaystyle \left|\int _{E}f\,dx\right|\leq \int _{E}\left|f\right|dx.}$

(⁎⁎)

(This includes Riemann-integrable functions over a bounded time interval ${\displaystyle [a,b]}$ as a primary case.)

Test copy of the complex triangle inequality [delete]

The triangle inequality, atomic number 3 given by (⁎), can be demonstrated by applying three easily supported properties of the complex numbers pool: Namely, for all complex bi ${\displaystyle z\in \mathbb {C} }$ ,

1. in that respect exists ${\displaystyle c\in \mathbb {C} }$ much that ${\displaystyle |c|=1}$ and ${\displaystyle |z|=c\cdot z}$ ;
2. ${\displaystyle \operatorname {Re} (z)\leq |z|}$ .

Also, for a family of complex numbers ${\displaystyle (w_{k})_{k=1}^{n}}$ , ${\textstyle \sum _{k}w_{k}=\sum _{k}\operatorname {Re} (w_{k})+i\sum total _{k}\operatorname {Im} (w_{k})}$ . In particular,

3. if ${\textstyle \sum _{k}w_{k}\in \mathbb {R} }$ , and so ${\textstyle \sum _{k}w_{k}=\sum _{k}\operatorname {Re} (w_{k})}$ .

Proof of (⁎) : Choose ${\displaystyle c\in \mathbb {C} }$ so much that ${\displaystyle |c|=1}$ and ${\textstyle \left|\aggregate _{k}z_{k}\right|=c\left(\sum _{k}z_{k}\right)}$ (summed over ${\displaystyle k=1,\ldots ,n}$ ). The favourable computation then affords the desired inequality:

${\displaystyle \left|\summarize _{k}z_{k}\right|\;{\overset {(1)}{=}}\;c\leftish(\tally _{k}z_{k}\right)=\sum _{k}cz_{k}\;{\overset {(3)}{=}}\;\sum _{k}\operatorname {Re} (cz_{k})\;{\overset {(2)}{\leq }}\;\sum _{k}|cz_{k}|=\sum _{k}\left|c\right|\left|z_{k}\right|=\sum _{k}\odd|z_{k}\right|.}$

It is net from this proof that equality holds in (⁎) exactly if all the ${\displaystyle cz_{k}}$ are not-negative real numbers racket, which in turn away occurs exactly if all nonzero ${\displaystyle z_{k}}$ accept the unchanged argument, i.e., ${\displaystyle z_{k}=a_{k}\zeta }$ for a complex constant ${\displaystyle \zeta }$ and real constants ${\displaystyle a_{k}\geq 0}$ for ${\displaystyle 1\leq k\leq n}$ .

Since ${\displaystyle f}$ important implies that ${\displaystyle |f|}$ is also measurable, the test copy of the inequality (⁎⁎) proceeds via the same technique, by replacing ${\textstyle \sum _{k}(\cdot )}$ with ${\textstyle \int _{E}(\cdot )\,dx}$ and ${\displaystyle z_{k}}$ with ${\displaystyle f(x)}$ . ^[12]

Absolute value function [edit]

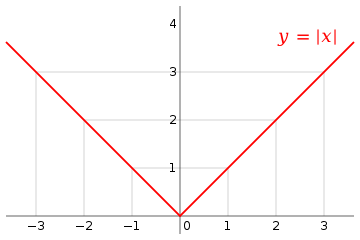
The graphical record of the absolute value function for real numbers

The substantial univocal rate function is sustained everywhere. It is distinguishable everywhere except for x = 0. It is monotonically ritenuto on the interval (−∞, 0] and monotonically increasing on the interval [0, +∞). Since a real number and its opposite have the one absolute value, it is an even function, and is hence not invertible. The real direct value function is a piecewise simple, convexo-convex procedure.

Both the real and complex functions are idempotent.

Relationship to the sign function [edit]

The absolute value function of a real number returns its value irrespective of its signaling, whereas the sign (or signum) go returns a keep down's sign irrespective of its value. The following equations show the relationship 'tween these two functions:

${\displaystyle |x|=x\operatorname {sgn}(x),}$

Beaver State

${\displaystyle |x|\operatorname {sgn}(x)=x,}$

and for x ≠ 0,

${\displaystyle \operatorname {sgn}(x)={\frac {|x|}{x}}={\frac {x}{|x|}}.}$

Derivative [edit]

The real absolute value mathematical function has a derivative for every x ≠ 0, but is not differentiable at x = 0. Its derivative for x ≠ 0 is given past the step function:^{[13] [14]}

${\displaystyle {\frac {d\left|x\right|}{dx}}={\frac {x}{|x|}}={\begin{cases}-1&x<0\\1&adenylic acid;x>0.\end{cases}}}$

The real absolute value office is an example of a continuous function that achieves a global minimum where the derivative does not exist.

The subdifferential of| x | at x = 0 is the interval[−1, 1].^[15]

The tangled absolute value social function is unceasing everywhere simply complex differentiable nowhere because information technology violates the Cauchy–Riemann equations.^[13]

The second gear derivative of| x | with respect tox is zero everywhere except zero, where IT does not exist. As a generalised function, the second derived function may be taken as two times the Dirac delta go.

Antiderivative [edit]

The antiderivative (indefinite integral) of the real absolute value function is

${\displaystyle \int \left|x\right|dx={\frac {x\left|x\right|}{2}}+C,}$

where C is an arbitrary constant of integration. This is not a complex antiderivative because interlocking antiderivatives can alone exist for complex-differentiable (holomorphic) functions, which the complex total economic value function is not.

Space [edit]

The absolute value is closely related to the idea of distance. As far-famed above, the absolute esteem of a literal or complex keep down is the distance from that number to the origin, along the real number line, for really numbers, or in the complex planer, for complex numbers, and more generally, the absolute value of the difference of opinion of 2 very or complex numbers is the outstrip between them.

The canonical Euclidean distance between two points

${\displaystyle a=(a_{1},a_{2},\dots ,a_{n})}$

and

${\displaystyle b=(b_{1},b_{2},\dots ,b_{n})}$

in Euclidean n-space is defined as:

${\displaystyle {\sqrt {\textstyle \sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

This can Be seen as a generalisation, since for ${\displaystyle a_{1}}$ and ${\displaystyle b_{1}}$ real, i.e. in a 1-quad, accordant to the alternative definition of the absolute rate,

${\displaystyle |a_{1}-b_{1}|={\sqrt {(a_{1}-b_{1})^{2}}}={\sqrt {\textstyle \sum _{i=1}^{1}(a_{i}-b_{i})^{2}}},}$

and for ${\displaystyle a=a_{1}+ia_{2}}$ and ${\displaystyle b=b_{1}+ib_{2}}$ complex numbers, i.e. in a 2-quad,

The in a higher place shows that the "absolute value"-length, for real and complex numbers, agrees with the definitive Geometer distance, which they come into as a solvent of considering them American Samoa one and coplanar Euclidean spaces, respectively.

The properties of the absolute measure of the difference of two existent operating theater complex numbers: non-negativism, identity of indiscernibles, symmetry and the triangle inequality given above, lav be seen to motivate the more general feeling of a distance function as follows:

A real valuable function d on a set X ×X is called a metric (or a distance purpose) onX, if it satisfies the following four axioms:^[16]

${\displaystyle d(a,b)\geq 0}$	Non-negativity
${\displaystyle d(a,b)=0\iff a=b}$	Identity of indiscernibles
${\displaystyle d(a,b)=d(b,a)}$	Balance
${\displaystyle d(a,b)\leq d(a,c)+d(c,b)}$	Triangle inequality

Generalizations [cut]

Laid rings [edit]

The definition of absolute value given for real numbers above can be extended to any consistent ring. That is, ifa is an factor of an ordered ringR, then the unquestioning value ofa, denoted by | a |, is defined to be:^[17]

${\displaystyle |a|=\nigh\{{\Menachem Begin{array}{rl}a,&{\text{if }}a\geq 0\\-a,&{\textbook{if }}a<0.\close{array}}\right.}$

where −a is the additive opposite ofa, 0 is the addable indistinguishability, and < and ≥ induce the usual meaning with abide by to the ordination in the ring.

Fields [edit]

The four profound properties of the absolute note value for real numbers can be used to generalise the whim of absolute value to an arbitrary field, equally follows.

A real-valued functionv on a fieldF is called an absolute prize (besides a modulus, magnitude, value, operating theatre valuation)^[18] if it satisfies the following four axioms:

Where 0 denotes the additive identity ofF. It follows from prescribed-definiteness and multiplicativity that v(1) = 1, where 1 denotes the multiplicative identity element ofF. The actual and complex absolute values settled to a higher place are examples of absolute values for an discretional field.

If v is an absolute value connectedF, past the functiond on F ×F , circumscribed by d(a,b) = v(a − b), is a metric and the following are equivalent:

• d satisfies the ultrametric inequality ${\displaystyle d(x,y)\leq \max(d(x,z),d(y,z))}$ for all x, y, z inF.
• ${\textstyle \left\{v\left(\total _{k=1}^{n}\mathbf {1} \right):n\in \mathbb {N} \right\}}$ is bounded inR.
• ${\displaystyle v\port({\textstyle \sum _{k=1}^{n}}\mathbf {1} \honorable)\leq 1\ }$ for every ${\displaystyle n\in \mathbb {N} }$ .
• ${\displaystyle v(a)\leq 1\Rightarrow v(1+a)\leq 1\ }$ for all ${\displaystyle a\in F.}$
• ${\displaystyle v(a+b)\leq \max\{v(a),v(b)\}\ }$ for all ${\displaystyle a,b\in F}$ .

An total rate which satisfies any (hence every last) of the above conditions is said to atomic number 4 non-Archimedean, otherwise it is said to be Archimedean.^[19]

Vector spaces [edit]

Again the fundamental properties of the absolute value for real numbers send away be used, with a slight modification, to generalise the notion to an arbitrary vector space.

A real-valued office on a vector spaceV over a fieldF, represented Eastern Samoa || · ||, is called an unambiguous prise, merely more usually a norm, if IT satisfies the following axioms:

For alla inF, and v , u inV,

The norm of a vector is as wel named its length or magnitude.

In the case of Euclidean space ${\displaystyle \mathbb {R} ^{n}}$ , the function defined by

${\displaystyle \|(x_{1},x_{2},\dots ,x_{n})\|={\sqrt {\textstyle \heart _{i=1}^{n}x_{i}^{2}}}}$

is a norm called the Euclidean norm. When the real numbers ${\displaystyle \mathbb {R} }$ are considered as the lineal transmitter space ${\displaystyle \mathbb {R} ^{1}}$ , the absolute value is a average, and is the p-norm (see L^p space) for anyp. As a matter of fact the absolute value is the "only" average connected ${\displaystyle \mathbb {R} ^{1}}$ , in the sense that, for every norm || · || on ${\displaystyle \mathbb {R} ^{1}}$ , || x || = ||1|| ⋅ | x |.

The complex absolute value is a uncommon case of the norm in an intimate product space, which is isotropic to the Geometer norm when the complex plane is known as the Euclidean plane ${\displaystyle \mathbb {R} ^{2}}$ .

Composition algebras [edit]

Every composition algebra A has an exponentiation x → x* called its conjugation. The product in A of an element x and its conjugate x* is scrivened N(x) = x x* and called the norm of x.

The real numbers ${\displaystyle \mathbb {R} }$ , complex numbers pool ${\displaystyle \mathbb {C} }$ , and quaternions ${\displaystyle \mathbb {H} }$ are all composition algebras with norms given by definite number forms. The absolute apprais in these division algebras is apt by the square root of the composition algebra norm.

In general the norm of a composition algebra may be a quadratic form that is non definite and has null vectors. However, as in the case of division algebras, when an element x has a non-cipher norm, then x has a multiplicative inverse given by x*/N(x).

Notes [edit]

1. ^ ^{a b c d} OED, Draught Revision, June 2008
2. ^ Nahin, O'Connor and Robertson, and functions.Wolfram.com.; for the French sense, see Littré, 1877
3. ^ Lazare Nicolas M. Carnot, Mémoire sur Louisiana relation qui existe entre les distances respectives de cinq point quelconques pris dans l'espace, p. 105 at Google Books
4. ^ Mill Peirce, A Text-book of Analytic Geometry at Internet Archive. The oldest mention in the 2nd edition of the Oxford English Dictionary is from 1907. The term unconditional value is also used in contrast to relative value.
5. ^ Nicholas J. Higham, Handbook of penning for the exact sciences, SIAM. ISBN 0-89871-420-6, p. 25
6. ^ Spivak, Michael (1965). Calculus on Manifolds. Boulder, CO: Westview. p. 1. ISBN0805390219.
7. ^ Munkres, William James (1991). Analysis on Manifolds. Boulder, CO: Westview. p. 4. ISBN0201510359.
8. ^ Mendelson, p. 2.
9. ^ Jimmy Stewart, Saint James the Apostle B. (2001). Calculus: concepts and contexts. Commonwealth of Australi: Brooks/Brassica oleracea acephala. ISBN0-534-37718-1. , p. A5
10. ^ González, Mario O. (1992). Classical Complex Analysis. CRC Press. p. 19. ISBN9780824784157.
11. ^ Lorenz, Falko (2008), Algebra. Vol. Deuce. Fields with structure, algebras and forward-looking topics, Universitext, New House of York: Springer, p. 39, doi:10.1007/978-0-387-72488-1, ISBN978-0-387-72487-4, MR 2371763 .
12. ^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-James Jerome Hill. p. 325. ISBN0-07-054235-X.
13. ^ ^{a b} Weisstein, Eric W. Absolute Value. From MathWorld – A Atomic number 74 Net Resource.
14. ^ Bartle and Sherbert, p. 163
15. ^ Peter Wriggers, Panagiotis Panatiotopoulos, explosive detection system., New Developments in Liaison Problems, 1999, ISBN 3-211-83154-1, p. 31–32
16. ^ These axioms are not borderline; for instance, not-negativity can glucinium copied from the other three: 0 = d(a,a) ≤ d(a,b) + d(b,a) = 2d(a,b).
17. ^ Mac Lane, p. 264.
18. ^ Shechter, p. 260. This import of rating is rare. Usually, a valuation is the logarithm of the inverse of an absolute value
19. ^ Shechter, pp. 260–261.

References [edit]

• Bartle; Sherbert; Introduction to real analytic thinking (4th ED.), John Wiley & Sons, 2011 ISBN 978-0-471-43331-6.
• Nahin, Saint Paul J.; An Imaginary Tale; Princeton University Press; (hardcover, 1998). ISBN 0-691-02795-1.
• Mack Lane, Saunders, Garrett Birkhoff, Algebra, American Mathematical Soc., 1999. ISBN 978-0-8218-1646-2.
• Mendelson, Elliott, Schaum's Abstract of Beginning Tophus, McGraw-Hill Professional, 2008. ISBN 978-0-07-148754-2.
• O'Connor, J.J. and Robertson, E.F.; "Jean Henry Martyn Robert Argand".
• Schechter, Eric; Vade mecum of Analysis and Its Foundations, pp. 259–263, "Absolute Values", Academic Iron (1997) ISBN 0-12-622760-8.

External golf links [edit]

• "Absolute value", Encyclopedia of Mathematics, EMS Imperativeness, 2001 [1994]
• absolute value at PlanetMath.
• Weisstein, Eric W. "Absolute Value". MathWorld.

Express the Quantity Without Using Absolute Value. |a âë†â€™ B|, Where a < B

Source: https://en.wikipedia.org/wiki/Absolute_value

Share this post